Excerpts, with commentary
by Steven H. Cullinane, from
http://bms.ulb.ac.be/Bulletin/98-2-3.pdf/polster.pdf
Burkard Polster
Pretty pictures of
geometries
Bull. Belg. Math. Soc. 5 (1998),
417-425
This research was supported by the Australian Research Council.
Received by the editors August 1997.
Communicated by James Hirschfeld.
1991 Mathematics Subject Classification:
51-01 -- Geometry, instructional exposition
51Exx -- Finite geometry and special incidence structures.
Key words and phrases: finite geometries, pictures.
Abstract
We present four construction principles that allow us to produce many
beautiful plane and spatial models of some of the most important small
finite geometries.
Introduction
....
In this note we describe four of the most useful construction
principles for constructing pictures of small incidence geometries
which capture large
parts of the abstract beauty of the geometries they depict. In order to
illustrate these construction principles, we use them to construct
models for some of the most important small geometries such as the Fano
plane, the generalized quadrangle of order 2, the Desargues
configuration and the projective space PG(3,2).
Why are good pictures important? Two of the main reasons that come to
mind are the following:
- To convey some of the abstract beauty of the objects we study to
people outside our field. This seems to be especially important today
as
it becomes more and more important to "justify" and "sell" the kind of
research we are fascinated by.
- Many of us think in terms of pictures of various degrees of
abstraction. The kind of pictures we want to concentrate on in this
note are immediately accessible and can serve to lure students into
studying incidence geometry and as a first step in teaching students
pictorial thinking in geometry.
Construction principles for pictures of small geometries
Whenever we are trying to create an appealing model of an abstract
geometry, we are trying to merge its abstract symmetries with spatial
symmetries.... We found that most... pictures, including the
traditional ones, can be made up using... simple rules.....
|
Construction
principle [1]:
number
right --> everything right
Given a small, highly symmetrical geometry with n points, look for the
same number of points arranged into a highly symmetrical spatial
object. Try to merge the two structures such that the symmetries of the
spatial object translate into symmetries of the geometry.
|
|
Construction
principle [2]:
subset geometries
Given a subset geometry on... n points, try to translate automorphisms
of symmetrical arrangements of n points in the plane or in space into
"good" models of the geometry which exhibit as many of these
automorphisms as possible. |
|
Construction
principle [3]:
subgeometry --> full geometry
Try to extend "good" models of subgeometries of a given geometry to a
"good" model of the full geometry. |
|
Construction
principle [4]:
geometry --> subgeometry
Try to find models of subgeometries of a given geometry "right in the
middle" of a good model of the geometry. |
Commentary
by S. H. Cullinane:
See The Diamond
Theorem,
Diamond Theory,
and Solomon's Cube.
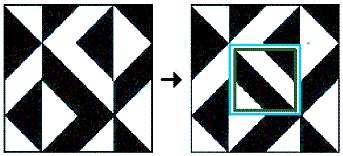
The proofs underlying properties described in these notes involve
extending symmetries of centrally located 2x2 or 2x2x2 subgeometries to
their larger 4x4 or 4x4x4 supergeometries.
|
References [by Polster]
[1] A. Beutelspacher. 21 - 6 = 15: a connection between
two
distinguished geometries. Amer.
Math. Monthly 93:29-41, 1986.
[2] A. Beutelspacher. A defense of the honour of an unjustly
neglected little geometry or a combinatorial approach to the projective
plane of order five. J. Geom.
30:182-195, 1987.
[3] D.R. Hughes and F.C. Piper. Design
Theory. Cambridge University Press, 1985.
[4] R.H. Jeurissen. Special sets of lines in PG(3,2). Linear Algebra Appl. 226-228:617-638,
1995.
[5] S.E. Payne. Finite generalized
quadrangles: a survey.
Proceedings of the International Conference on Projective Planes (Washington State Univ.,
Pullman, Wash., 1973), pp. 219-261. Washington State Univ. Press,
Pullman,
Wash., 1973.
[6] S.E. Payne and J.A. Thas. Finite
generalized quadrangles,
Research Notes in Math. 110.
Pitman, Boston, 1984.
[7] B. Polster. A geometrical
picture book. Universitext series, Springer-Verlag, to appear.
Burkard Polster
Department of Pure Mathematics
The University of Adelaide
South Australia 5005
Page created December 2, 2004.
