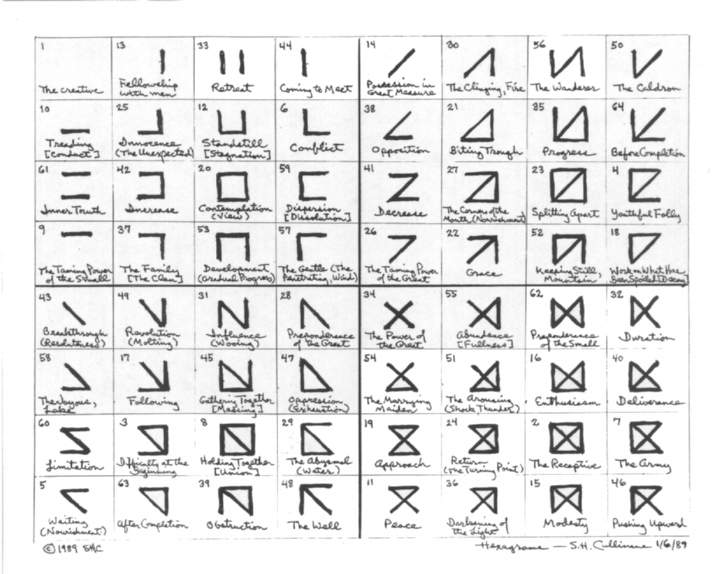
| This site gives a new
arrangement of the 64 hexagrams of the I Ching. The new arrangement
lets us describe the natural group of transformations of these
hexagrams in a simple way. This arrangement was discovered during an
investigation of the six-dimensional affine space over the
two-element field by S. H. Cullinane on January 6, 1989.
For an updated version of this page, see my new math site, finitegeometry.org/sc/. The updated page there is at http://finitegeometry.org/sc/64/iching.html. |
|
|
Geometry of the I Ching |
| Introduction - Hesse on the I Ching and on the chessboard: |
| "Once Knecht confessed
to his teacher that he wished to learn enough to be able to
incorporate the system of the I Ching into the Glass Bead Game."
- Magister Ludi (The Glass Bead Game), by Hermann Hesse (1943), tr. by Richard and Clara Winston, Bantam paperback, 1970, p. 117 "Here and there in the ancient literatures we encounter legends
of wise and mysterious games that were conceived and played by
scholars, monks, or the courtiers of cultured princes. These might
take the form of chess games in which the pieces and squares had
secret meanings in addition to their usual functions." |
| Hermann
Hesse and Glass Bead Game Design Das Glasperlenspiel |
| The Cullinane sequence of the 64 hexagrams: |
| 01 13 33 44 14 30 56
50 10 25 12 06 38 21 35 64 61 42 20 59 41 27 23 04 09 37 53 57 26 22 52 18 43 49 31 28 34 55 62 32 58 17 45 47 54 51 16 40 60 03 08 29 19 24 02 07 05 63 39 48 11 36 15 46 |
| The above system of "chessboard" coordinates gives a 3-dimensional Karnaugh map if we interpret the four 4x4 quadrants of the 8x8 array, counted clockwise from the upper left, as the four layers, counted top to bottom, of a 4x4x4 cube. Then (with identification of opposite sides of the overall cube) each subcube is bordered by six other subcubes, each of which differs from the given subcube in exactly one coordinate. |
| Explanation of Karnaugh maps Karnaugh maps/Carroll diagrams, by Greg Gamble A (Lewis) Carroll diagram - predecessor of the 1953 Karnaugh maps |
| The I Ching as affine coordinates in a 4x4x4 cube: |
| The above labeling of the 64 subcubes of a 4x4x4 cube enables us to describe the natural transformations of the I Ching hexagrams in a geometrically simple way. See the following research note on affine groups and references on affine geometry. |
| Affine Groups on Small Binary Spaces, by S. H.
Cullinane Affine geometries compared with other geometries (from Cut-the-Knot) Ordering information for Geometry and Symmetry, by Paul B. Yale |
| The von Franz style of drawing hexagrams: |
| An alternative way of
drawing the I Ching hexagrams is suggested by Marie-Louise von
Franz. Draw a figure of six lines made up of the four sides and the
two diagonals of a square. "They are the same six lines that exist in the I Ching.... Now observe the square more closely: four of the lines are of equal length, the other two are longer.... For this reason symmetry cannot be statically produced and a dance results." - Marie-Louise von Franz, Number and Time (1970), Northwestern U. Press paperback, 1979, p. 108 One may identify the above six lines with the yin (broken) lines
of I Ching hexagrams as follows: |
| Ordering information for books by Marie-Louise von
Franz |
| References on the I Ching: |
| Related sites by S. H. Cullinane: |
Note of January 6, 1989 showing
the 64 hexagrams in the von Franz
style,
in the arrangement discovered by S. H. Cullinane:
|
|
| Page last updated May
14, 2004; created August 8, 2000.
|