Symmetry of Walsh Functions

by Steven H. Cullinane

Walsh functions have an inherent symmetry that is best seen by regarding the non-constant Walsh functions as hyperplanes in finite geometry. Such symmetry is exhibited by the 15 affine hyperplanes of the 4-space over the 2-element field.

For definitions of Walsh functions, see The first sixteen Walsh functions and Mathworld -- Walsh Function.

For an excellent introduction to Walsh functions, by Benjamin Jacoby (pdf format), click here.

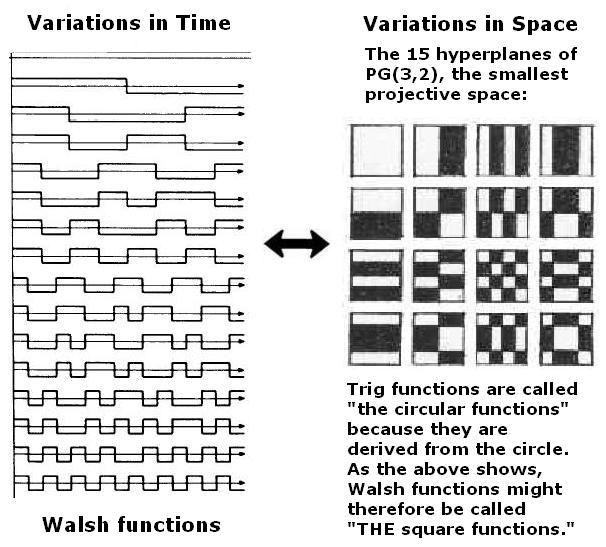
The above illustration shows that
the first 16 Walsh functions
(from Jacoby's article)
are isomorphic to the 16 parts of the figure
in the following research note:

A related picture may be found on page 573
of A New Kind of Science, by Stephen Wolfram
(Wolfram Media, 2002):

This is a larger set of Walsh functions,
based on an 8x8 square.
Note that the 16 pictures
in the upper left quadrant
are essentially the same as
the 16 pictures in my 1986 note.

For more on symmetry properties in finite geometry, see Diamond Theory.

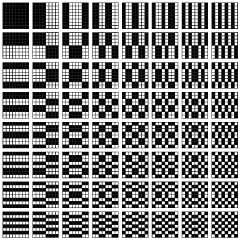
For another picture showing the equivalence of nonconstant Walsh functions with the 15 affine hyperplanes that account for 4x4 symmetry in diamond theory, see the 15 "stencils" in Fig. VIII-8 of Shift Register Sequences, by Solomon W. Golomb, Holden-Day, 1967 (Revised edition published by Aegean Park Press, 1982).

For a picture showing a set of Walsh functions arranged in various visually striking ways, see Mathworld -- Walsh Function.

For a bibliography of the theory of Walsh functions, click here.

For a bibliography of the applications of Walsh functions, click here.

For some philosophical remarks
related to Walsh functions, see

The Grid of Time.

Page last maintained Sept. 14, 2004; created August 31, 2001.
Counter started Nov. 4, 2005.