The Fano Plane
Revisualized:

or, The Eightfold Cube
by Steven H. Cullinane

or, The Eightfold Cube
by Steven H. Cullinane
Here is the usual model of the seven points and seven lines (including the circle) of the smallest finite projective plane (the Fano plane):

The above model indicates with great clarity six symmetries of the plane-- those it shares with the equilateral triangle. It does not, however, indicate where the other 162 symmetries come from.
Shown below is a new model of this same projective plane, using partitions of cubes to represent points:

The cubes' partitioning planes are added in binary (1+1=0) fashion. Three partitioned cubes are collinear if and only if their partitioning planes' binary sum equals zero.
The second model is useful because it lets us generate naturally all 168 symmetries of the Fano plane by splitting a cube into a set of four parallel 1x1x2 slices in the three ways possible, then arbitrarily permuting the slices in each of the three sets of four. See examples below.
The second model is useful because it lets us generate naturally all 168 symmetries of the Fano plane by splitting a cube into a set of four parallel 1x1x2 slices in the three ways possible, then arbitrarily permuting the slices in each of the three sets of four. See examples below.
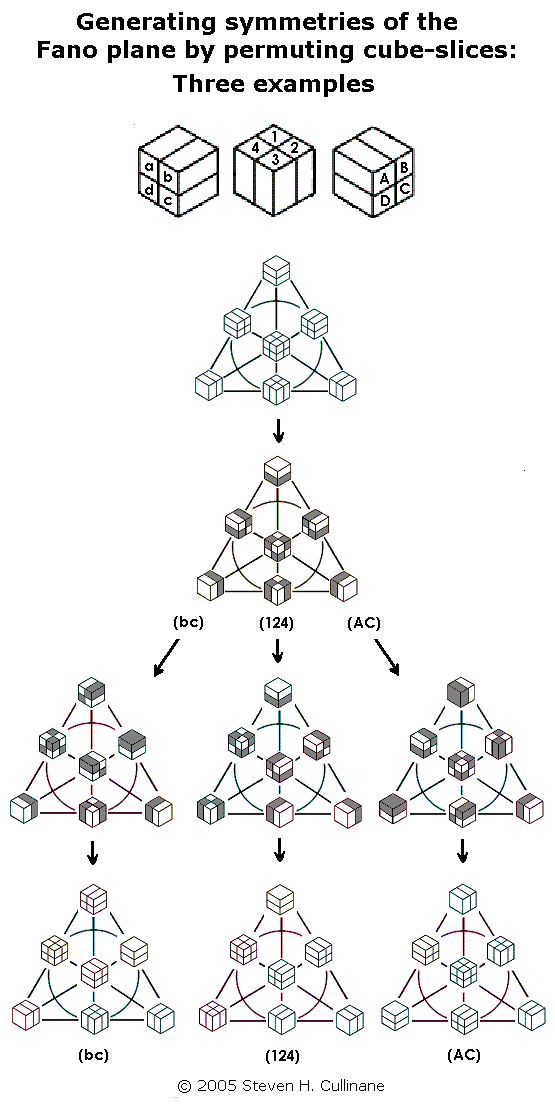
For a proof that such permutations generate the 168 symmetries, see Binary Coordinate Systems.
(Note that this procedure, if regarded as acting on the set of eight individual subcubes of each cube in the diagram, actually generates a group of 168*8 = 1,344 permutations. But the group's action on the diagram's seven partitions of the subcubes yields only 168 distinct results. This illustrates the difference between affine and projective spaces over the binary field GF(2). In a related 2x2x2 cubic model of the affine 3-space over GF(2) whose "points" are individual subcubes, the group of eight translations is generated by interchanges of parallel 2x2x1 cube-slices. This is clearly a subgroup of the group generated by permuting 1x1x2 cube-slices. Such translations in the affine 3-space have no effect on the projective plane, since they leave each of the plane model's seven partitions-- the "points" of the plane-- invariant.)
(Note that this procedure, if regarded as acting on the set of eight individual subcubes of each cube in the diagram, actually generates a group of 168*8 = 1,344 permutations. But the group's action on the diagram's seven partitions of the subcubes yields only 168 distinct results. This illustrates the difference between affine and projective spaces over the binary field GF(2). In a related 2x2x2 cubic model of the affine 3-space over GF(2) whose "points" are individual subcubes, the group of eight translations is generated by interchanges of parallel 2x2x1 cube-slices. This is clearly a subgroup of the group generated by permuting 1x1x2 cube-slices. Such translations in the affine 3-space have no effect on the projective plane, since they leave each of the plane model's seven partitions-- the "points" of the plane-- invariant.)
To view the cubes model in a wider context, see Galois Geometry, Block Designs, and Finite-Geometry Models.
For another application of the points-as-partitions technique, see The Diamond Theorem and Latin-Square Geometry: Orthogonal Latin Squares as Skew Lines.
For more on the plane's symmetry group in another guise, see John Baez on Klein's Quartic Curve and the online book The Eightfold Way. For more on the mathematics of cubic models, see Solomon's Cube.
For another application of the points-as-partitions technique, see The Diamond Theorem and Latin-Square Geometry: Orthogonal Latin Squares as Skew Lines.
For more on the plane's symmetry group in another guise, see John Baez on Klein's Quartic Curve and the online book The Eightfold Way. For more on the mathematics of cubic models, see Solomon's Cube.
For a large downloadable folder with many other related web pages, see Notes on Finite Geometry.
Page created May 4, 2005.