The Miracle Octad Generator
(MOG) of R T. Curtis

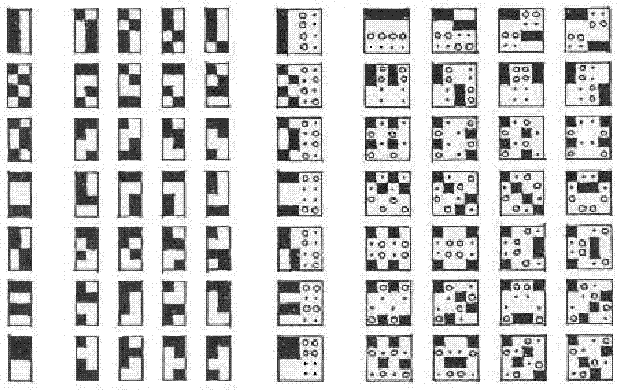
The image “http://www.log24.com/theory/images/MOGCurtisPlain.gif” cannot be displayed, because it contains errors.

Shown above is a rearranged version of the
Miracle Octad Generator (MOG) of R. T. Curtis
("A new combinatorial approach to M24,"
Math. Proc. Camb. Phil. Soc., 79 (1976), 25-42.)

The MOG is a pairing of the 35 partitions of an 8-set into two 4-sets with the 35 partitions of AG(4,2) (the affine 4-space over GF(2)) into 4 affine planes.  The pairing preserves certain incidence properties.  It is used in studying the Steiner system S(5,8,24), the large Mathieu group, the extended binary Golay code, the Leech lattice, and subgroups of the Monster.

History:

This pairing, without illustrations, was apparently first described in 1910 by G. M. Conwell in "The 3-space PG(3,2) and its group," Ann. of Math. 11 (1910) 60-76.

The 35 square structures above apparently first appeared, without any reference to their role in finite geometry, in the 1976 Curtis paper mentioned above.

The 35 square structures above were discovered independently in 1976 by Steven H. Cullinane.  The role they play in finite geometry was apparently first described by Cullinane in an AMS abstract in 1979 that was received for publication on Oct. 31, 1978. The connection between finite geometry and the square structures illustrated above was also pointed out by Cullinane in a note, "Orthogonal Latin Squares as Skew Lines," of December 1978.  (For related material, see Latin-Square Geometry.)  The existence of the 35 combinatorially defined square structures of Curtis was pointed out by Curtis to Cullinane in a personal communication of March 1979.  The connection between the finite-geometry research of Conwell and the combinatorial research of Curtis was apparently first pointed out in "Generating the Octad Generator," a note by Cullinane of April 28, 1985.

Curtis uses the MOG to construct the Steiner system S(5,8,24), a structure that goes back at least to Witt in 1938 and possibly (Rotman, An Introduction to the Theory of Groups) to Carmichael in 1931.  Uenal Mutlu cites specific papers that seem to be relevant:  R. D. Carmichael, "Tactical configurations of rank two," Amer. J. Math. 53 (1931) 217-240, and E. Witt, "Ueber Steinersche Systeme," Abh. Math. Sem. Hansischen Univ. 12 (1938) 265-275.

Related material:
  1. Shane Kelly's "Mathieu Groups, the Golay Code and Curtis' Miracle Octad Generator" (pdf), which has a MOG illustration, apparently from Sphere Packings, Lattices and Groups, by Conway and Sloane, that differs from the original Curtis MOG by a mirror reflection.

    From Conway and Sloane

    The first edition of the Conway-Sloane book was published in 1988. Conway and Sloane supply a brief discussion of the square structures in the Curtis MOG as pictures of the finite geometry AG(4,2), but make no reference to the work of Cullinane.

  2. Steven H. Cullinane, Geometry of the 4x4 Square and The Diamond Theorem.

  3. Thomas M. Thompson, From Error-Correcting Codes through Sphere Packings to Simple Groups. Mathematical Association of America, Washington, 1983.
"While the reader may draw many a moral from our tale,
I hope that the story is of interest for its own sake.
Moreover, I hope that it may inspire others, participants
or observers, to preserve the true and complete record of
our mathematical times."

-- Thomas M. Thompson, op. cit.


Page created Nov. 30, 2005, by Steven H. Cullinane.