The Grid and the Quilt

From a 2002 review by Stacy G. Langton of Sherman Stein's book on mathematics, How the Other Half Thinks:

"The title of Stein's book (perhaps chosen by the publisher?) seems to refer to the popular left brain/right brain dichotomy. As Stein writes (p. ix): 'I hope this book will help bridge that notorious gap that separates the two cultures: the humanities and the sciences, or should I say the right brain (intuitive, holistic) and the left brain (analytical, numerical). As the chapters will illustrate, mathematics is not restricted to the analytical and numerical; intuition plays a significant role.' Stein does well to avoid identifying mathematics with the activity of just one side of the brain. He would have done better, however, not to have endorsed the left brain/right brain ideology. While it does indeed appear to be the case that the two sides of our brain act in rather different ways, the idea that the right brain is 'intuitive, holistic,' while the left brain is 'analytical, numerical,' is a vast oversimplification, and goes far beyond the actual evidence."

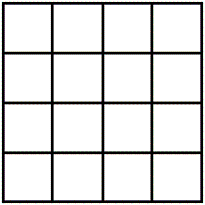
Despite the evidence, it is tempting to view the pictures below as illustrating, on the left, the line-diagram side, a cold, analytical approach to a mathematical theory, and, on the right, the colored-pattern side, a warm, intuitive approach to the same theory -- the grid (left) versus the quilt (right), as it were.

Galois Geometry
The Simplest Examples

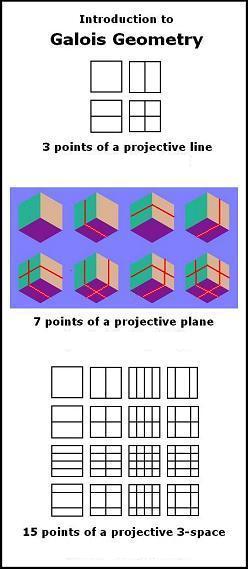"Projective spaces over a finite field, otherwise known as Galois geometries, find wide application in coding theory, algebraic geometry, design theory, graph theory, and group theory as well as being beautiful objects of study in their own right."

-- Oxford University Press on
General Galois Geometries, by
J. W. P. Hirschfeld and J. A. Thas

The simplest Galois geometries are the projective spaces of one, two, and three dimensions over the two-element Galois field... That is to say, the binary projective line, plane, and 3-space.

Perhaps the simplest models for such geometries are those of Diamond Theory.

The pictures at left show these models.

The pictures at right illustrate some graphic designs with underlying structures based on models like those shown at left.

Click on any of the pictures at right for an introduction, Theme and Variations, to the aesthetics of designs based on Galois geometry.

The appearance of the pictures at right explains the origin of the title "Diamond Theory."

The line diagrams at left are related to the two-color patterns at right as follows.

The three line diagrams above result from the three partitions, into pairs of 2-element sets, of the 4-element set from which the entries of the bottom colored figure are drawn. Taken as a set, these three line diagrams describe the structure of the bottom colored figure. After coordinatizing the figure in a suitable manner, we find that this set of three line diagrams is invariant under the group of 16 binary translations acting on the colored figure.

A more remarkable invariance -- that of symmetry itself -- is observed if we arbitrarily and repeatedly permute rows and/or columns and/or 2x2 quadrants of the colored figure above. Each resulting figure has some ordinary or color-interchange symmetry. The cause of this symmetry-invariance in the colored patterns is the symmetry-invariance of the line diagrams under a group of 322,560 binary affine transformations.

-- Steven H. Cullinane