Sunday, January 29, 2006 10:00 AM
The eye's plain version is a thing apart,
The vulgate of experience. Of this,
A few words, an and yet, and yet, and yet--
As part of the never-ending meditation,
Part of the question that is a giant himself:
Of what is this house composed if not of the sun,
These houses, these difficult objects, dilapidate
Appearances of what appearances,
Words, lines, not meanings, not communications,
Dark things without a double, after all,
Unless a second giant kills the first--
A recent imagining of reality,
Much like a new resemblance of the sun,
Down-pouring, up-springing and inevitable,
A larger poem for a larger audience,
As if the crude collops came together as one,
A mythological form, a festival sphere,
A great bosom, beard and being, alive with age.
-- Wallace Stevens, opening lines of
"An Ordinary Evening in New Haven"
Sunday, January 29, 2006 9:00 AM
In the punctual centre of all circles white
Stands truly....

... and Bloom with his vast accumulation
Stands and regards and repeats the primitive lines.
-- Wallace Stevens,
"From the Packet of Anacharsis"
Related material:
Balanchine's Birthday.
Sunday, January 29, 2006 8:00 AM

Today is the Chinese New Year, 4074.
Saturday, January 28, 2006 12:48 PM
Memorial ofSt. Thomas Aquinas:
Joyce and Aquinas,
by William T. Noon, S. J.
St. Thomas Aquinas,
by G. K. Chesterton
Log24, Epiphany 2006
Friday, January 27, 2006 8:25 AM
Mozart, 2006Mozart, 1935
Poet, be seated at the piano.
Play the present, its hoo-hoo-hoo,
Its shoo-shoo-shoo, its ric-a-nic,
Its envious cachinnation.
If they throw stones upon the roof
While you practice arpeggios,
It is because they carry down the stairs
A body in rags.
Be seated at the piano.
That lucid souvenir of the past,
The divertimento;
That airy dream of the future,
The unclouded concerto . . .
The snow is falling.
Strike the piercing chord.
Be thou the voice,
Not you. Be thou, be thou
The voice of angry fear,
The voice of this besieging pain.
Be thou that wintry sound
As of the great wind howling,
By which sorrow is released,
Dismissed, absolved
In a starry placating.
We may return to Mozart.
He was young, and we, we are old.
The snow is falling
And the streets are full of cries.
Be seated, thou.
-- Wallace Stevens, Ideas of Order (1936)
From the center:
"'Mozart, 1935' immediately discloses a will to counter complaints of pure poetry, to refute that charge heard regularly from Stevens's critics, to find 'his particular celebration out of tune today' on his own if necessary; and, in short, to meet the communist [poet and critic Willard] Maas's 'respect for his magnificent rhetoric' at least halfway across from right to left."
-- Alan Filreis, Modernism from Right to Left: Wallace Stevens, the Thirties, and Literary Radicalism (Cambridge: Cambridge University Press, 1994), p. 211
From the left:
Norman Lebrecht on this year's celebration of the 250th anniversary of Mozart's birth (January 27, 1756):
"... Mozart, it is safe to say, failed to take music one step forward....
... Mozart merely filled the space between staves with chords that he knew would gratify a pampered audience. He was a provider of easy listening, a progenitor of Muzak....
... He lacked the rage of justice that pushed Beethoven into isolation, or any urge to change the world. Mozart wrote a little night music for the ancien regime. He was not so much reactionary as regressive....
... Little in such a mediocre life gives cause for celebration....
... The bandwaggon of Mozart commemorations was invented by the Nazis in 1941....
... In this orgy of simple-mindedness, the concurrent centenary of Dmitri Shostakovich-- a composer of true courage and historical significance-- is being shunted to the sidelines, celebrated by the few.
Mozart is a menace to musical progress, a relic of rituals that were losing relevance in his own time and are meaningless to ours. Beyond a superficial beauty and structural certainty, Mozart has nothing to give to mind or spirit in the 21st century. Let him rest. Ignore the commercial onslaught. Play the Leningrad Symphony. Listen to music that matters."
The left seems little changed since 1935.
Thursday, January 26, 2006 9:00 AM
On Beauty
"Something beautiful fills the mind yet invites the search for something beyond itself, something larger or something of the same scale with which it needs to be brought into relation. Beauty, according to its critics, causes us to gape and suspend all thought. This complaint is manifestly true: Odysseus does stand marveling before the palm; Odysseus is similarly incapacitated in front of Nausicaa; and Odysseus will soon, in Book 7, stand 'gazing,' in much the same way, at the season-immune orchards of King Alcinous, the pears, apples, and figs that bud on one branch while ripening on another, so that never during the cycling year do they cease to be in flower and in fruit. But simultaneously what is beautiful prompts the mind to move chronologically back in the search for precedents and parallels, to move forward into new acts of creation, to move conceptually over, to bring things into relation, and does all this with a kind of urgency as though one's life depended on it."

The above symbol of Apollo suggests, in accordance with Scarry's remarks, larger structures. Two obvious structures are the affine 4-space over GF(3), with 81 points, and the affine plane over GF(32), also with 81 points. Less obvious are some related projective structures. Joseph Malkevitch has discussed the standard method of constructing GF(32) and the affine plane over that field, with 81 points, then constructing the related Desarguesian projective plane of order 9, with

Miniquaternion geometry: An introduction to the study of projective planes, by T. G. Room and P. B. Kirkpatrick. Cambridge Tracts in Mathematics and Mathematical Physics, No. 60. Cambridge University Press, London, 1971. viii+176 pp.For "miniquaternions" of a different sort, see my entry on Visible Mathematics for Hamilton's birthday last year:

Wednesday, January 25, 2006 4:00 PM
and playing
with a full deck:

Alicia Keys
"... it's going to be
accomplished in steps,
this establishment
of the Talented in
the scheme of things."
-- Anne McCaffrey,
Radcliffe '47,
To Ride Pegasus
(And born yesterday...
Neil "I am, I cried" Diamond)
Tuesday, January 24, 2006 7:00 AM
for Michael Harris
(See previous entry.)

Related material:
A classic book in a postmodern
("free-floating signs") cover --

This is my Princeton Companion
to Mathematics, from the days
when Princeton University Press
had higher scholarly standards.
Monday, January 23, 2006 6:00 PM
In Defense of Hilbert(On His Birthday)
Michael Harris (Log24, July 25 and 26, 2003) in a recent essay, Why Mathematics? You Might Ask (pdf), to appear in the forthcoming Princeton Companion to Mathematics:
"Mathematicians can... claim to be the first postmodernists: compare an art critic's definition of postmodernism-- 'meaning is suspended in favor of a game involving free-floating signs'-- with Hilbert's definition of mathematics as 'a game played according to certain simple rules with meaningless marks on paper.'"
Harris adds in a footnote:
"... the Hilbert quotation is easy to find but is probably apocryphal, which doesn't make it any less significant."
If the quotation is probably apocryphal, Harris should not have called it "Hilbert's definition."
For a much more scholarly approach to the concepts behind the alleged quotation, see Richard Zach, Hilbert's Program Then and Now (pdf):
[Weyl, 1925] described Hilbert's project as replacing meaningful mathematics by a meaningless game of formulas. He noted that Hilbert wanted to 'secure not truth, but the consistency of analysis' and suggested a criticism that echoes an earlier one by Frege: Why should we take consistency of a formal system of mathematics as a reason to believe in the truth of the pre-formal mathematics it codifies? Is Hilbert's meaningless inventory of formulas not just 'the bloodless ghost of analysis'?"
Some of Zach's references:
[Ramsey, 1926] Frank P. Ramsey. Mathematical logic. The Mathematical Gazette, 13:185-94, 1926. Reprinted in [Ramsey, 1990, 225-244].
[Ramsey, 1990] Frank P. Ramsey. Philosophical Papers, D. H. Mellor, editor. Cambridge University Press, Cambridge, 1990
From Frank Plumpton Ramsey's Philosophical Papers, as cited above, page 231:
"... I must say something of the system of Hilbert and his followers.... regarding higher mathematics as the manipulation of meaningless symbols according to fixed rules....
Mathematics proper is thus regarded as a sort of game, played with meaningless marks on paper rather like noughts and crosses; but besides this there will be another subject called metamathematics, which is not meaningless, but consists of real assertions about mathematics, telling us that this or that formula can or cannot be obtained from the axioms according to the rules of deduction....
Now, whatever else a mathematician is doing, he is certainly making marks on paper, and so this point of view consists of nothing but the truth; but it is hard to suppose it the whole truth."
[Weyl, 1925] Hermann Weyl. Die heutige Erkenntnislage in der Mathematik. Symposion, 1:1-23, 1925. Reprinted in: [Weyl, 1968, 511-42]. English translation in: [Mancosu, 1998a, 123-42]....
[Weyl, 1968] Hermann Weyl. Gesammelte Abhandlungen, volume 1, K. Chandrasekharan, editor. Springer Verlag, Berlin, 1968.
[Mancosu, 1998a] Paolo Mancosu, editor. From Brouwer to Hilbert. The Debate on the Foundations of Mathematics in the 1920s. Oxford University Press, Oxford, 1998.
From Hermann Weyl, "Section V: Hilbert's Symbolic Mathematics," in Weyl's "The Current Epistemogical Situation in Mathematics," pp. 123-142 in Mancosu, op. cit.:"What Hilbert wants to secure is not the truth, but the consistency of the old analysis. This would, at least, explain that historic phenomenon of the unanimity amongst all the workers in the vineyard of analysis.
To furnish the consistency proof, he has first of all to formalize mathematics. In the same way in which the contentual meaning of concepts such as "point, plane, between," etc. in real space was unimportant in geometrical axiomatics in which all interest was focused on the logical connection of the geometrical concepts and statements, one must eliminate here even more thoroughly any meaning, even the purely logical one. The statements become meaningless figures built up from signs. Mathematics is no longer knowledge but a game of formulae, ruled by certain conventions, which is very well comparable to the game of chess. Corresponding to the chess pieces we have a limited stock of signs in mathematics, and an arbitrary configuration of the pieces on the board corresponds to the composition of a formula out of the signs. One or a few formulae are taken to be axioms; their counterpart is the prescribed configuration of the pieces at the beginning of a game of chess. And in the same way in which here a configuration occurring in a game is transformed into the next one by making a move that must satisfy the rules of the game, there, formal rules of inference hold according to which new formulae can be gained, or 'deduced,' from formulae. By a game-conforming [spielgerecht] configuration in chess I understand a configuration that is the result of a match played from the initial position according to the rules of the game. The analogue in mathematics is the provable (or, better, the proven) formula, which follows from the axioms on grounds of the inference rules. Certain formulae of intuitively specified character are branded as contradictions; in chess we understand by contradictions, say, every configuration which there are 10 queens of the same color. Formulae of a different structure tempt players of mathematics, in the way checkmate configurations tempt chess players, to try to obtain them through clever combination of moves as the end formula of a correctly played proof game. Up to this point everything is a game; nothing is knowledge; yet, to use Hilbert's terminology, in 'metamathematics,' this game now becomes the object of knowledge. What is meant to be recognized is that a contradiction can never occur as an end formula of a proof. Analogously it is no longer a game, but knowledge, if one shows that in chess, 10 queens of one color cannot occur in a game-conforming configuration. One can see this in the following way: The rules are teaching us that a move can never increase the sum of the number of queens and pawns of one color. In the beginning thissum = 9, and thus-- here we carry out an intuitively finite [anschaulich-finit] inference through complete induction-- it cannot be more than this value in any configuration of a game. It is only to gain this one piece of knowledge that Hilbert requires contentual and meaningful thought; his proof of consistency proceeds quite analogously to the one just carried out for chess, although it is, obviously, much more complicated.
It follows from our account that mathematics and logic must be formalized together. Mathematical logic, much scorned by philosophers, plays an indispensable role in this context."
Constance
Reid says it was not Hilbert himself, but his critics, who described
Hilbert's formalism as reducing mathematics to "a meaningless game,"
and quotes the Platonist Hardy as saying that Hilbert was ultimately
concerned not with meaningless marks on paper, but with ideas:
"Hilbert's program... received its share of criticism. Some mathematicians objected that in his formalism he had reduced their science to 'a meaningless game played with meaningless marks on paper.' But to those familiar with Hilbert's work this criticism did not seem valid.
'... is it really credible that this is a fair account of Hilbert's view,' Hardy demanded, 'the view of the man who has probably added to the structure of significant mathematics a richer and more beautiful aggregate of theorems than any other mathematician of his time? I can believe that Hilbert's philosophy is as inadequate as you please, but not that an ambitious mathematical theory which he has elaborated is trivial or ridiculous. It is impossible to suppose that Hilbert denies the significance and reality of mathematical concepts, and we have the best of reasons for refusing to believe it: "The axioms and demonstrable theorems," he says himself, "which arise in our formalistic game, are the images of the ideas which form the subject-matter of ordinary mathematics."'"
-- Constance Reid in Hilbert-Courant, Springer-Verlag, 1986 (The Hardy passage is from "Mathematical Proof," Mind 38, 1-25, 1929, reprinted in Ewald, From Kant to Hilbert.)
Harris concludes his essay with a footnote giving an unsourced Weyl quotation he found on a web page of David Corfield:
".. we find ourselves in [mathematics] at exactly that crossing point of constraint and freedom which is the very essence of man's nature."
One source for the Weyl quotation is the above-cited book edited by Mancosu, page 136. The quotation in the English translation given there:
"Mathematics is not the rigid and petrifying schema, as the layman so much likes to view it; with it, we rather stand precisely at the point of intersection of restraint and freedom that makes up the essence of man itself."
Corfield says of this quotation that he'd love to be told the original German. He should consult the above references cited by Richard Zach.
For more on the intersection of restraint and freedom and the essence
of man's nature, see the Kierkegaard chapter cited in the previous
entry.
Monday, January 23, 2006 12:00 PM
The CaseAn entry suggested by today's New York Times story by Tom Zeller Jr., A Million Little Skeptics:
From The Hustler, by Walter Tevis:
The only light in the room was from the lamp over the couch where she was reading.
He looked at her face. She was very drunk. Her eyes were swollen, pink at the corners. "What's the book?" he said, trying to make his voice conversational. But it sounded loud in the room, and hard.
She blinked up at him, smiled sleepily, and said nothing.
"What's the book?" His voice had an edge now.
"Oh," she said. "It's Kierkegaard. Soren Kierkegaard." She pushed her legs out straight on the couch, stretching her feet. Her skirt fell back a few inches from her knees. He looked away.
"What's that?" he said.
"Well, I don't exactly know, myself." Her voice was soft and thick.
He turned his face away from her again, not knowing what he was angry with. "What does that mean, you don't know, yourself?"
She blinked at him. "It means, Eddie, that I don't exactly know what the book is about. Somebody told me to read it, once, and that's what I'm doing. Reading it."
He looked at her, tried to grin at her-- the old, meaningless, automatic grin, the grin that made everybody like him-- but he could not. "That's great," he said, and it came out with more irritation than he had intended.
She closed the book, tucked it beside her on the couch. "I guess this isn't your night, Eddie. Why don't we have a drink?"
"No." He did not like that, did not want her being nice to him, forgiving. Nor did he want a drink.
Her smile, her drunk, amused smile, did not change. "Then let's talk about something else," she said. "What about that case you have? What's in it?" Her voice was not prying, only friendly. "Pencils?"
"That's it," he said. "Pencils."
She raised her eyebrows slightly. Her voice seemed thick. "What's in it, Eddie?"
"Figure it out yourself." He tossed the case on the couch.
Soren Kierkegaard on necessity and possibility
in The Sickness Unto Death, Chapter 3,
The Diamond of Possibility,
the Baseball Almanac,
and this morning's entry, "Natural Hustler."
Monday, January 23, 2006 3:57 AM
Natural Hustler (jpg, 283 KB)Sunday, January 22, 2006 2:08 PM
"Our Town" premiered at the
McCarter Theatre, Princeton University.
Related material:
St. Patrick's Day, 2005,
St. Patrick's Day, 2003,
and, for
Piper Laurie's birthday
(today) in 2003,
Through a Soda-Fountain
Mirror, Darkly.

Sunday, January 22, 2006 7:00 AM
(continued)
Alms for Oblivion:

In memory of Akkadian scholar
Erica Reiner, who died at 81 on
December 31, 2005.
-- Gil Stein, director of the Oriental Institute at the University of Chicago
was scheduled for
Friday the 13th
at the church of
"doubting Thomas"--
St. Thomas the Apostle
in Chicago.
Sunday, January 22, 2006 4:07 AM
Saturday, January 21, 2006 7:48 AM
Jews on FictionSee Tony Kushner and E.L. Doctorow in today's New York Times, Rebecca Goldstein's talk from last summer's Mykonos conference on mathematics and narrative, and Martin Buber on the Bible.
Friday, January 20, 2006 12:00 PM
"Wherefore let it hardly... be... thought that the prisoner... was at his best a onestone parable... for... pathetically few... cared... to doubt... the canonicity of his existence as a tesseract."
-- Finnegans Wake, page 100, abridged
"... we have forgotten that we were angels and painted ourselves into a corner of resource extraction and commodification of ourselves."
-- A discussion, in a draft of
a paper (rtf) attributed
to Josh Schultz,
of the poem "Diamond"
by Attila Jozsef
Commodification of
the name Cullinane:
See the logos at
cullinane.com,
a design firm with
the motto

To adapt a phrase from
Finnegans Wake, the
"fourstone parable" below
is an attempt to
decommodify my name.
Fourstone Parable:
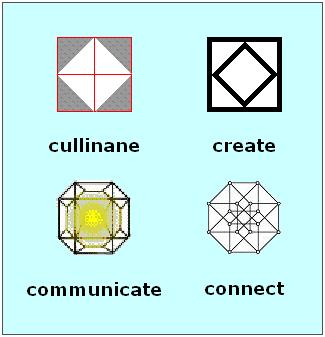
(See also yesterday's "Logos."
The "communicate" logo is taken from
an online library at Calvin College;
the "connect" logo is a commonly
available picture of a tesseract
(Coxeter, Regular Polytopes, p. 123),
and the other two logos
are more or less original.)
For a more elegant
four-diamond figure, see
Jung and the Imago Dei.
Thursday, January 19, 2006 9:00 AM
Logos

 Alvin Plantinga |
 Philosophy logo |
 Harry Plantinga |
 CCEL logo |
 Madeleine L'Engle |
 Tesseract logo |
Thursday, January 19, 2006 7:48 AM
"Wallace Stevens's remarkable oeuvre is a quasi-spiritual quest for the supreme fiction, for a poetry that 'must take the place / Of empty heaven and its hymns' and thus help modern man find meaning in a godless world. The poet's role, for Stevens, is that of high priest of the imagination: it is the poet who 'gives to life the supreme fictions without which we are unable to conceive of it.' ....
... Stevens's hallmark 'imagination-reality' complex... is pursued almost obsessively in his poetry and prose of the 1940s. Parts of a World, published in 1942, and the poem-sequence of the same year, 'Notes toward a Supreme Fiction' ('Notes' was subsequently collected in Transport to Summer in 1947), comprise a prolonged meditation in a time of war on poetry and the poet's role, in the face of what Stevens, in his essay 'The Noble Rider and the Sound of Words,' terms 'the pressure of reality.' Parts of a World is riven by its competing vocabularies. A discourse of desire, of process, of the poet's contemplation of the mind in the act of finding what will suffice, is elaborated in 'the never-resting mind' of 'The Poems of Our Climate' and in 'The Well Dressed Man with a Beard,' in which 'It can never be satisfied, the mind, never' [occurs]. A very different idiom, that of the 'hero' or 'major man,' the figure of capable imagination, dominates and directs such poems as 'Mrs Alfred Uruguay,' 'Asides on the Oboe' and 'Examination of the Hero in a Time of War,' where
Summer, jangling
the savagest diamonds and
Dressed in its
azure-doubled crimsons,
May truly bear
its heroic fortunes
For the large,
the solitary figure."
-- Lee M. Jenkins,
University College Cork,
"Wallace Stevens,"
The Literary Encyclopedia,
9 Dec., 2004.
For some related serious, but less solemn, remarks, click on the above date.
Thursday, January 19, 2006 6:23 AM
at Breakfast
-- G. K. Chesterton, Orthodoxy
Inscapes.
For Shakespeare:
Hopkins on Inscape.
For both:

Click on the picture
for related remarks.
Tuesday, January 17, 2006 12:00 PM

BBC News Jan. 17
Related material:
Log24 Sept. 27 and
Sept. 28, 2005,
as well as
The Harvard Crimson,
Jan. 13, 2006:
"President was resolute--
'This is bullshit'"

Monday, January 16, 2006 4:00 AM
Mathematics and NarrativeRebecca Goldstein, Mathematics and the Character of Tragedy:
"It was Plato who best expressed-- who veritably embodied-- the tension between the narrative arts and mathematics."
Veritably.

